Divergence and Curl

Circulation Density. The circulation density of \(\vec{F}\) at a point \(P\) in the direction of a unit vector \(\vec{n}\) is a scalar measurement of the strength of circulation (or rotation) of \(\vec{F}\) around \(P\) perpendicular to \(\vec{n}\) in the direction determined by the right hand rule, see Figure 3.1 and Figure 3.2.

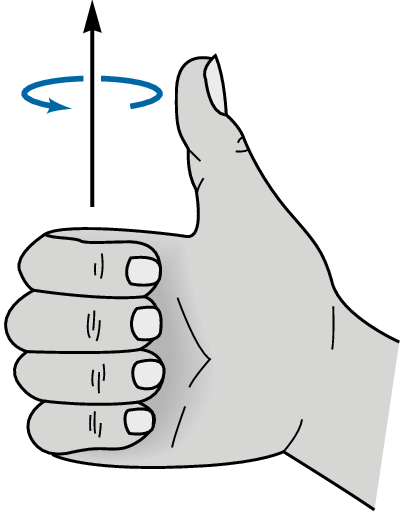
• Positive if \(\vec{F}\) induces a rotation around the point \(P\) in the direction given by the right hand rule (think of placing a little paddle-wheel like the one shown in Figure 3.3 at \(P\) in the plane perpendicular to \(\vec n\text{,}\) will the vectors close to \(P\) on the plane force the paddle-wheel to rotate? If so, will the paddle-wheel rotate in the direction determined by the right hand rule?)

  

• Negative if \(\vec{F}\) induces a rotation around the point \(P\) in the opposite direction given by the right hand rule.

• \(0\) if there if there is no induced rotation around \(P\text{.}\)

The stronger the induced rotation, the larger the magnitude of the circulation density.

Geometric Definition of Curl. The curl of a vector field \(\vec{F}\) in \(3\)-space at a point \((x,y,z)\) and denoted \({\rm curl}\, \vec{F}(x,y,z)\) is defined to be the vector with the following properties:

• It points in direction of greatest circulation density at \((x,y,z)\text{.}\)

• Its magnitude is equal to the circulation density at \((x,y,z)\text{.}\)

Cartesian coordinate definition of Curl. For \(\vec{F} =F_1\vec{i} +F_2\vec{j} +F_3\vec{k}{\text ,}\) we define

The Scalar Curl. Though curl is defined for vector fields in \(3\)-space, it is useful to have a compatible definition in \(2\)-space.

• Geometric Definition of the Scalar Curl: The scalar curl of \(\vec{F} =F_1\vec{i} +F_2\vec{j}\) around the point \((x,y)\) is a scalar measurement of the induced counterclockwise rotation of \(\vec{F}\) around \((x,y)\text{.}\) It is positive if the vectors in \(\vec{F}\) induce a counterclockwise rotation around \((x,y)\text{,}\) and negative they induce a clockwise rotation.

• Cartesian Coordinate Definition of the Scalar Curl: For \(\vec{F} =F_1\vec{i} +F_2\vec{j}\text{,}\) we define the scalar curl of \(\vec{F}\) as

  \begin{equation*} \text{Scalar curl of } \vec{F}=\displaystyle\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y} \text{.} \end{equation*}

A vector field \(\vec{G}\) is called a curl field if it is the curl of some other field \(\vec{F}\) i.e. \(\vec{G} ={\rm curl}\, \vec{F}\text{.}\)

If \(f(x,y,z)\) has continuous second order partial derivatives then \({\rm curl}\, \nabla f =\vec{0}\text{.}\) In particular, this tells us that a vector field with non-zero curl cannot be conservative.

If \({\rm curl}\, \vec{F}(x,y,z)=\vec{0}\) at a point \((x,y,z)\text{,}\) we say \(\vec{F}\) is \(irrotational\) at \((x,y,z)\text{.}\) If \(\vec{F}\) is irrotational at all points, we say it is a curl-free vector field.

Geometric Definition of Divergence. The divergence of a vector field \(\vec{F}\) at a point \((x,y,z)\) is a scalar measurement of the flow of the vectors in \(\vec{F}\) through \((x,y,z)\text{.}\) It is:

• Positive if the vectors in \(\vec{F}\) generally flow away from \((x,y,z)\text{,}\) and they stronger the flow away, the larger the magnitude.

• Negative if the vectors in \(\vec{F}\) generally flow into \((x,y,z)\text{,}\) and the stronger they flow into \((x,y,z)\text{,}\) the larger the magnitude.

• \(0\) if there if there is no flow in or out of \((x,y,z)\text{,}\) or if the flow into \((x,y,z)\) cancels with the flow out of \((x,y,z)\text{.}\)

Cartesian Coordinate Definition of the Divergence. For \(\vec{F} =F_1\vec{i} +F_2\vec{j} +F_3\vec{k}\) we define

More generally, for a vector field \(\vec{F}\) in any dimension, we define \({\rm div} \vec{F} =\nabla \cdot \vec{F}\text{.}\)

If \(\vec{F}(x,y,z)\) has continuous second order partial derivatives then \({\rm div (curl}\, \vec{F} )=0\text{.}\) In particular, this tells us that a vector field with non-zero divergence cannot be a curl field.